유클리드와 아인슈타인과 무대_손재서
페이지 정보
작성자 최고관리자 조회2,232회 작성일 17-09-28 11:08본문
글빨 17.09.28
유클리드와 아인슈타인과 무대
손재서
고대 그리스의 수학자 유클리드(B.C. 330~275)는 『원론』에서 기하학의 기초를 정의와 정리와 공준으로 구분하였다. 그의 책으로 인하여 수학은 증명이라는 반석 위에 오르게 되었으며, 때문에 오늘날 수많은 수포자들을 양산하는 계기가 되었다. 그러나 어떤 수학자들은 유클리드의 증명을 세상에서 가장 아름다운 이론이라며 수학을 희한하게도 미학적 대상으로 바라보기도 한다는데, 범인에게는 이를 알아볼 눈이 없으니 그건 그들의 개인적 취향으로 남겨두기로 하자.
오늘 할 이야기는 평행선 공준이라고 불리는 유클리드의 말도 많고 탈도 많은 제 5공준에 대한 이야기이다.
유클리드의 공준
1. 임의의 점으로부터 다른 임의의 점에 대해 직선을 그을 수 있다.
2. 임의의 직선을 계속 연장할 수 있다.
3. 임의의 중심과 반지름을 가진 원을 그릴 수 있다.
4. 모든 직각은 서로 같다.
5. 두 직선이 한 직선과 만날 때, 같은 쪽에 있는 내각의 합이 2직각(180˚)보다 작으면 이 두 직선을 연장할 때 2직각보다 작은 내각을 이루는 쪽에서 반드시 만난다.
이처럼 5개의 공준 중에서 다른 4개와는 달리 다섯 번째 공준은 일단 말이 많다. 말 많으면 공산당이라는 옛말도 있지만, 옛날 사람들도 말이 많은 것들에 대해서는 일단 의심의 눈초리를 보냈던 모양이다. 공준이란 단순, 단단, 단아함을 미덕으로 삼을 진데 이건 뭐 공준이라기보다는 다른 공준으로부터 유도되는 증명이 아닐까 하는 의심을 유클리드 이후 수학자라는 사람들은 계속하였다. 많은 수학자들이 제 5공준이 공준이 아님을 증명해보려 하였지만 19세기가 되어서야 인류는 수학적으로 이것을 해내게 되었다. 어떻게? 보여이, 로바쳅스키, 리만과 같은 수학자들은 유클리드가 기획한 공간이 아니라 다른 공간을 볼 수 있었기에 이것이 가능해졌던 것이다.
그런데 현재 우리 공연예술가들은 유클리드의 공간과 다른 공간을 상상하고 있는가? 상상할 수 있는가? 공연예술을 위해 수학을 배워야 한다는 이야기는 아니니 미리 겁먹지는 마시라.
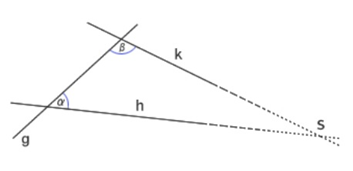
<그림 1> 평행선 공준
위 그림에서 각 α와 각 β의 합이 180˚보다 작으면 선분 k와 h는 점 s에서 만난다는 것이 평행선 공준이다. 이게 무슨 귀신 씨나락 까먹는 소리냐 싶겠지만 수학을 좋아하는 어떤 사람들은 평행선 공준과 다른 4개의 공준만 가지고 삼각형의 내각의 합이 180˚라는 것을 증명해 낼 수 있다고 한다. 그래서 뭐?
“삼각형의 내각의 합은 180˚이다”
평행선 공준과 동치(그 말이 그 말, 이리저리 돌려 말하지만 같은 말이라는 것을 수학에서는 동치라고 한다)인 명제들이 여럿 있는데 이것도 그 중 하나이다. 이 말은 참일까 거짓일까? 유클리드의 공간에서는 참이고 다른 공간에서는 거짓이다. 다음 그림을 보자.
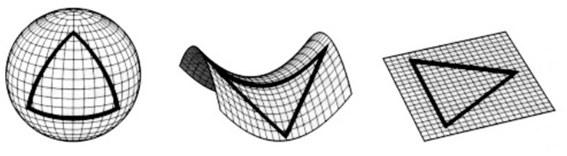
<그림 2> 서로 다른 곡률공간의 삼각형
세 번째 삼각형의 내각의 합은 정확히 180˚이지만, 첫 번째의 경우는 내각의 합이 180˚보다 크고, 두 번째의 경우는 180˚보다 작다. 3가지 서로 다른 공간의 차이는 수학자들이 곡률이라고 부르는 것에서 기인한다. 유클리드 공간의 경우는 곡률이 0이고 구의 경우 곡률이 양의 값을 가지며, 말안장 모양의 경우 곡률이 음의 값을 가진다.
세 번째는 평면도형이고 앞의 2가지는 입체도형이라 그런 것 아니냐고? 그렇게 간단한 문제가 아니다. 유클리드의 원론은 입체도형에 대해서도 기술하고 있다. 우리가 포기했던 고등학교 수학의 공간도형, 벡터 단원은 모두 유클리드 기하학에 그 근원을 두고 있다.
문제는 공간이 휘어져 있다는 생각이다. 아인슈타인은 휘어진 공간이라는 아이디어를 이용하여 일반상대성이론을 이끌어 내었다. 질량을 가진 물체는 중력을 가지고 주변의 공간을 휘게 한다. 아인슈타인의 이 이론에 따르면 질량(에너지)1)을 가진 무대 위의 배우는 중력으로 무대와 객석을 휘게 또는 일그러지게 하면서 연기할 수 있다.
이 가능성에도 불구하고 우리의 무대는, 우리의 객석은 아직도 유클리드 공간에 머무르고 있지는 않은가?
무대 위의 배우는 주변 공간을 얼마만큼 휘게 하는가? 무대 위의 소품은 무대와 객석을 얼마만큼 일그러지게 하는가?
이제 우리는 연기할 때, 무대를 구성할 때, 에너지의 유동에 따른 공간의 곡률을 고민해 보아야 하지 않을까?
1) E=mc2?이라는 특수상대성이론에 따르면 물질은 에너지로 전환된다.
- 극단 자갈치 배우
